Câu hỏi:
27/02/2024 46,572
Đáp án chính là: B
Kẻ tại H.
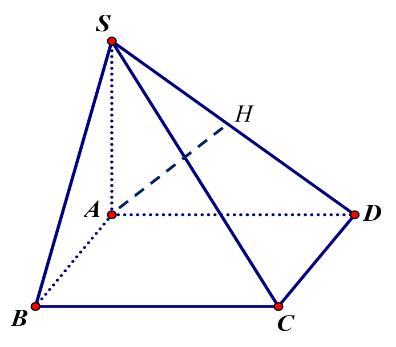
Dễ thấy .
Mà Þ .
Suy rời khỏi .
Áp dụng hệ thức lượng nhập có:
.
Vậy .
Nhà sách VIETJACK:
🔥 Đề đua HOT:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
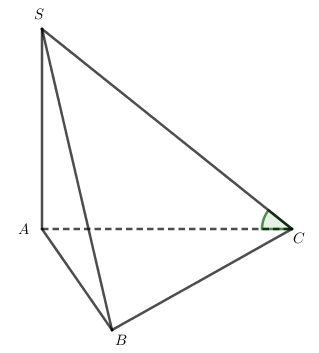
Cho hình chóp S.ABC sở hữu ; tam giác ABC đều cạnh a và SA = a. Tìm góc thân thích SC và mặt mày phẳng lì (ABC).
Câu 2:
Tập nghiệm của bất phương trình là
Câu 3:
Trên mặt mày phẳng lì tọa chừng, biết tập trung điểm trình diễn những số phức z thỏa mãn nhu cầu là một đàng tròn trĩnh. Tâm của đàng tròn trĩnh tê liệt sở hữu tọa chừng là
Câu 4:
Cho hàm số có đồ đua là đàng cong nhập hình mặt mày.
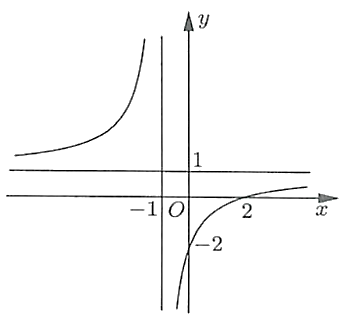
Toạ chừng gửi gắm điểm của đồ vật thị hàm số vẫn cho tới và trục tung là:
Câu 5:
Trong không khí Oxyz, góc thân thích nhì mặt mày phẳng lì (Oxy) và (Oyz) bằng
Câu 6:
Có từng nào độ quý hiếm nguyên vẹn của thông số để hàm số đồng biến đổi bên trên khoảng
