Công thức tính diện tích hình tam giác và ứng dụng thực tế

Công thức tính diện tích S hình tam giác là gì?

Công thức tính diện tích S của tam giác là S = (a x h) / 2. Trong số đó, a là chừng lâu năm lòng của tam giác và h là độ cao kể từ đỉnh vuông góc cho tới lòng của tam giác. Để tính diện tích S tam giác, tớ nhân chừng lâu năm lòng với độ cao, tiếp sau đó phân tách thành phẩm cho tới 2.

Ví dụ phương pháp tính S tam giác:

Tính diện tích S tam giác có tính lâu năm lòng là 5m và độ cao là 24dm.

Giải: 

Chiều cao 24dm = 2,4m

Áp dụng công thức tính diện tích S tam giác tớ có:

S tam giác =(5 x 2.4)/2 = 6m2

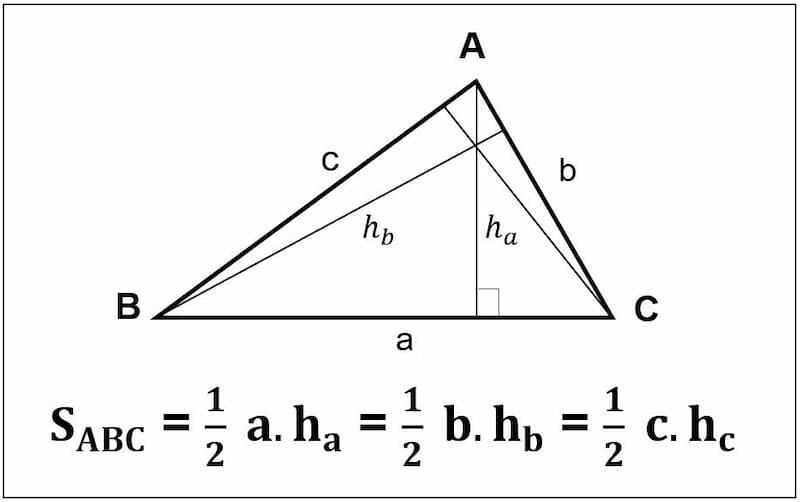
Có từng nào loại tam giác?

Tam giác hoàn toàn có thể được phân loại theo đòi vô số phương pháp không giống nhau, dựa vào những điểm lưu ý của những cạnh và góc. Dưới đấy là 7 loại tam giác phổ biến:

1. Tam giác vuông là tam giác sở hữu một góc vì như thế 90 chừng. Hai cạnh tạo thành góc vuông được gọi là cạnh góc vuông, còn cạnh còn sót lại được gọi là cạnh huyền.
2. Tam giác cân là tam giác sở hữu nhì cạnh cân nhau. Hai cạnh cân nhau này được gọi là cạnh mặt mày, còn cạnh còn sót lại được gọi là cạnh lòng.
3. Tam giác đều là tam giác sở hữu cả tía cạnh cân nhau.
4. Tam giác nhọn là tam giác sở hữu toàn bộ tía góc nhỏ rộng lớn 90 chừng.
5. Tam giác tù là tam giác sở hữu một góc to hơn 90 chừng.
6. Tam giác thường là tam giác không tồn tại cạnh và góc nào là cân nhau.
7. Tam giác vuông cân là tam giác vừa phải vuông vừa phải cân nặng, tức là sở hữu cả nhì cạnh góc vuông và nhì cạnh mặt mày cân nhau.

Dưới đấy là những công thức tính diện tích S tam giác khá đầy đủ và cụ thể nhất nhưng mà chúng ta có thể tìm hiểu thêm.

Cách tính diện tích S tam giác cân

Diện tích hình tam giác cân S vì như thế tích của độ cao nối kể từ đỉnh tam giác cơ cho tới cạnh lòng tam giác, tiếp sau đó phân tách cho tới 2: S = (a x h)/ 2. Trong đó: a là chiều lâu năm lòng tam giác cân nặng và h là độ cao của tam giác.

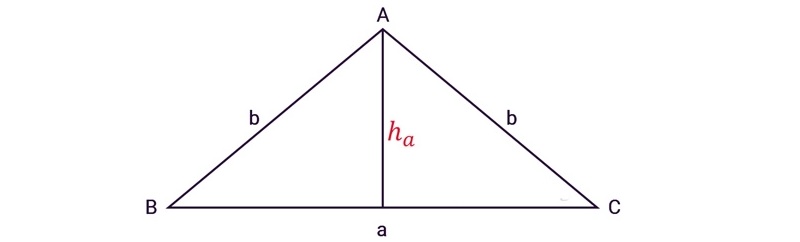
Ví dụ: Tính diện tích S tam giác cân nặng có:

a, Độ lâu năm cạnh lòng vì như thế 6cm và lối cao vì như thế 7cm

b, Độ lâu năm cạnh lòng vì như thế 5m và lối cao vì như thế 3,2m

Lời giải:

a, Diện tích của hình tam giác là:

S tam giác = (6 x 7) : 2 = 21 (cm2)

Đáp số: 21cm2

b, Diện tích của hình tam giác là:

S tam giác = (5 x 3,2) : 2 = 8 (m2)

Đáp số: 8m2

Công thức tính diện tích S tam giác đều

Diện tích hình tam giác đều (hay s tam giác đều) vì như thế tích độ cao và cạnh lòng, tiếp sau đó phân tách cho tới 2: S = (a x h)/ 2. Trong đó: a là hiều lâu năm lòng tam giác đều (đáy là một trong những nhập 3 cạnh của tam giác) và h là hiều cao của tam giác (chiều cao tam giác vì như thế đoạn trực tiếp hạ kể từ đỉnh xuống đáy)

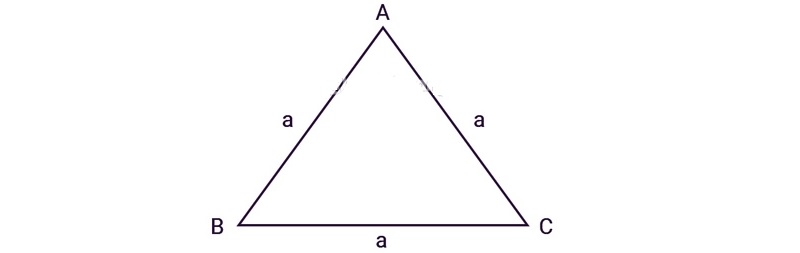
Ví du: Tính diện tích S của tam giác đều có:

a, Độ lâu năm một cạnh tam giác vì như thế 6cm và lối cao vì như thế 10cm

b, Độ lâu năm một cạnh tam giác vì như thế 4cm và lối cao vì như thế 5cm

Lời giải

a, Diện tích hình tam giác là:

(6 x 10) : 2 = 30 (cm2)

Đáp số: 30cm2

b, Diện tích hình tam giác là:

(4 x 5) : 2 = 10 (cm2)

Đáp số: 10cm2

Cách tính diện tích S tam giác vuông

Công thức tính diện tích S tam giác vuông bằng ½ tích của độ cao với chiều lâu năm đáy: S = (a x b)/ 2. Trong đó: a và b là chừng lâu năm 2 cạnh góc vuông. Vì tam giác vuông sở hữu 2 cạnh góc vuông, nên chiều cao tiếp tục ứng với một cạnh góc vuông, cùng theo với chiều lâu năm lòng tiếp tục ứng với cạnh góc vuông còn sót lại.

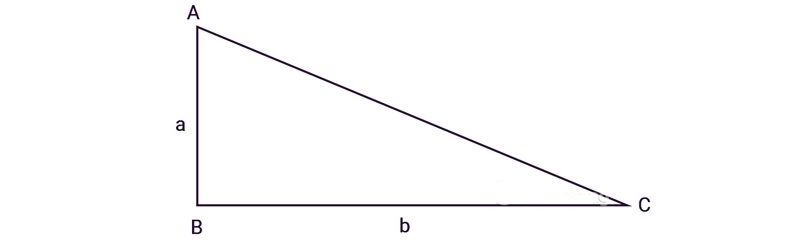
Ví dụ: Tính diện tích S của tam giác vuông có:

a, Hai cạnh góc vuông thứu tự là 3cm và 4cm

b, Hai cạnh góc vuông thứu tự là 6m và 8m

Lời giải:

a, Diện tích của hình tam giác là:

S tam giác = (3 x 4) : 2 = 6 (cm2)

Đáp số: 6cm2

b, sát dụng phương pháp tính diện tích S tam giác tớ có:

S tam giác =(6 x 8) : 2 = 24 (m2)

Đáp số: 24m2

Công thức tính diện tích S tam giác vuông cân

Tam giác vuông cân nặng là tam giác vừa phải vuông, vừa phải cân nặng. Cách tính diện tích S hình tam giác vuông cân nặng là S = một nửa x a^2. Trong đó: a là chừng lâu năm cạnh lòng của tam giác. 

Công thức tính diện tích S tam giác nhập hệ tọa chừng Oxyz

Trên lý thuyết, tớ hoàn toàn có thể người sử dụng những công thức tính tam giác phẳng phiu cho tới tam giác nhập không khí Oxyz. Nhưng vì vậy tiếp tục bắt gặp nhiều trở ngại Khi đo lường. Vậy nên, nhập không khí Oxyz, tớ tiếp tục tính diện tích S tam giác phụ thuộc vào tích được đặt theo hướng.

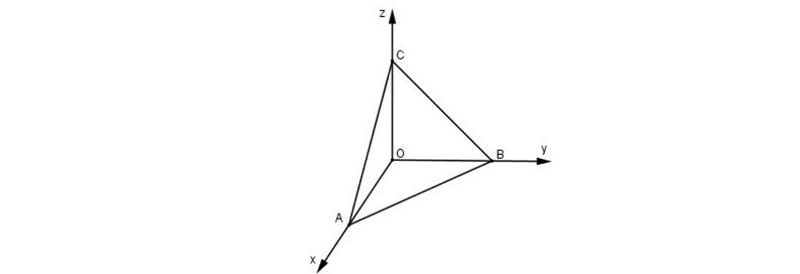
Trong không khí Oxyz, cho tới tam giác ABC. Diện tích tam giác ABC được xem theo đòi công thức: 

Ví dụ minh họa:

Trong không khí Oxyz, cho tới tam giác ABC sở hữu tọa chừng tía đỉnh thứu tự là A(-1;1;2), B(1;2;3), C(3;-2;0). Tính diện tích S tam giác ABC.

Bài giải:

Kiến thức nên nhớ nhằm học tập chất lượng tốt phương pháp tính diện tích S hình tam giác

Để thực hiện chất lượng tốt bài bác luyện về phong thái tính diện tích S hình tam giác, bạn phải ghi lưu giữ một số trong những nội dung cần thiết sau đây.

Khái niệm hình tam giác

Hình tam giác là một trong những mô hình cơ phiên bản nhập hình học tập, sở hữu tía đỉnh là tía điểm ko trực tiếp mặt hàng và tía cạnh là tía đoạn trực tiếp nối những đỉnh cùng nhau. Đặc trưng cần thiết của tam giác là tổng tía góc nhập một tam giác nên luôn luôn vì như thế 180 chừng.

Các đặc điểm cơ phiên bản của hình tam giác

1. Tính hóa học về góc của hình tam giác:

Tổng tía góc nhập một tam giác luôn luôn vì như thế 180 chừng. Ví dụ: Ta ký hiệu những góc nhập tam giác là A, B và C, thì A + B + C = 180 chừng.

2. Tính hóa học về cạnh của hình tam giác:

Hay còn được gọi là bất đẳng thức tam giác. Tổng chừng lâu năm nhì cạnh của tam giác luôn luôn to hơn chừng lâu năm cạnh còn sót lại. Vấn đề này hoàn toàn có thể được màn trình diễn như sau: a + b > c, b + c > a, c + a > b. (Trong đó: a, b, c thứu tự là những cạnh của một hình tam giác.)

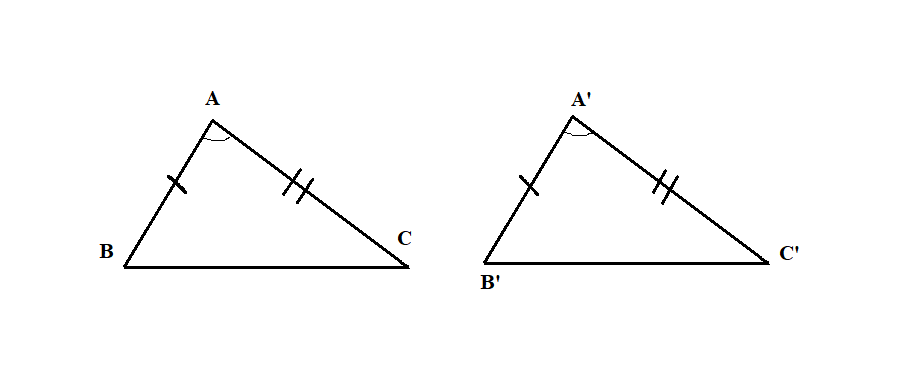
3. Hai tam giác vì như thế nhau:

Hai tam giác được gọi là cân nhau (hay đồng dạng) Khi những cạnh và những góc của bọn chúng ứng cân nhau. Vấn đề này tức là những cặp cạnh ứng của nhì tam giác có tính lâu năm cân nhau và những cặp góc ứng cũng đều có độ quý hiếm cân nhau.

4. Đường cao của hình tam giác:

Hình tam giác sở hữu tía lối cao, là những lối vuông góc với những cạnh và trải qua những đỉnh ứng.

5. Đường trung tuyến của hình tam giác:

Hình tam giác sở hữu tía lối trung tuyến, là những lối nối những đỉnh với trung điểm của những cạnh ứng.

Ký hiệu hình tam giác nhập toán học

Trong toán học tập, hình tam giác thông thường được ký hiệu vì như thế những vần âm ghi chép thông thường hoặc vần âm hoa gạch men bên dưới. Có một số trong những ký hiệu thông dụng được dùng nhằm biểu thị tam giác, như:

• Sử dụng những vần âm ghi chép thường: Tam giác ABC, nhập cơ A, B, C là tía đỉnh của tam giác.
• Sử dụng những vần âm ghi chép hoa gạch men dưới: Tam giác ΔABC, nhập cơ Δ thay mặt cho tới hình tam giác và A, B, C là tía đỉnh của tam giác.
• Sử dụng chỉ số: Tam giác ABC, nhập cơ A, B, C sở hữu chỉ số bên dưới nhằm chỉ đỉnh ứng. Ví dụ: A1B2C3.

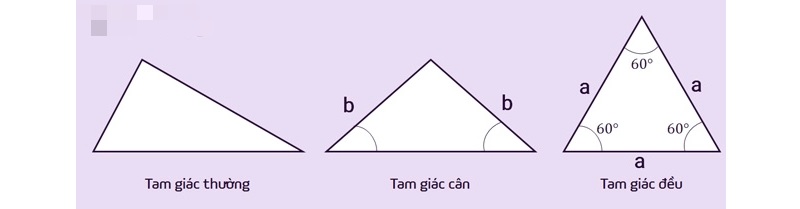
Các loại tam giác thông thường gặp

Hình tam giác được phân trở nên nhiều loại dựa vào điểm lưu ý của những cạnh và những góc. Cụ thể như sau:

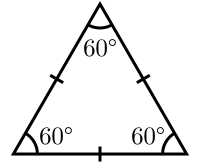
Tam giác đều

Tam giác đều là tam giác sở hữu cả tía cạnh và tía góc cân nhau. Tất cả những góc nhập tam giác đều đều phải có độ quý hiếm 60 chừng.

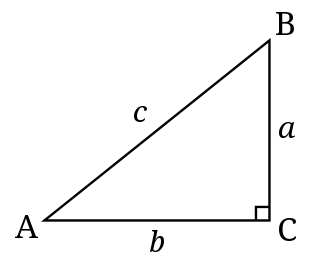
Tam giác vuông

Tam giác vuông sở hữu một góc vuông, tức là một trong những góc có mức giá trị đúng là 90 chừng.

Tam giác cân

Tam giác cân nặng là tam giác sở hữu tối thiểu nhì cạnh cân nhau. Vấn đề này đồng nghĩa tương quan với việc sở hữu tối thiểu nhì góc cân nhau.

Tam giác vuông cân

Tam giác vuông cân nặng là tam giác sở hữu một góc vuông và nhì cạnh sát vuông cân nhau.

Tam giác nhọn

Tam giác nhọn là tam giác sở hữu toàn bộ tía góc đều nhọn, tức là có mức giá trị nhỏ rộng lớn 90 chừng.

Tam giác tù

Tam giác tù là tam giác sở hữu một góc tù, tức là một trong những góc có mức giá trị to hơn 90 chừng.

Các dạng bài bác luyện phương pháp tính diện tích S tam giác cơ phiên bản và nâng cao

Đối với kỹ năng về hình tam giác, tùy vào cụ thể từng cấp cho học tập sẽ sở hữu những dạng bài bác luyện riêng rẽ. Nhưng với những bé xíu đang được nhập giới hạn tuổi cấp cho 1, tiếp tục thông thường bắt gặp những dạng bài bác thói quen diện tích S của hình tam giác như sau:

Dạng 1: Cách tính diện tích S tam giác lúc biết chừng lâu năm lòng và chiều cao

Đối với dạng bài bác luyện này, đề bài bác thông thường tiếp tục cho tới dữ khiếu nại về độ cao và chừng lâu năm cạnh lòng. Nên những em chỉ việc vận dụng công thức tính tam giác thông thường nhằm mò mẫm rời khỏi đáp án đúng đắn.

Ví dụ: Tính diện tích S tam giác thông thường và tam giác vuông có:

a) Độ lâu năm lòng vì như thế 32cm và độ cao vì như thế 25cm.

b) Hai cạnh góc vuông có tính lâu năm thứu tự là 3dm và 4dm.

Lời giải:

a) Diện tích hình tam giác là:

S = 32 x 25 : 2 = 400 (cm2)

b) Diện tích hình tam giác là:

S = 3 x 4 : 2 = 6 (dm2)

Đáp số: a) 400cm2; b) 6dm2

Dạng 2: Tính chừng lâu năm lòng lúc biết diện tích S hình tam giác và chiều cao

Ở dạng bài bác luyện này, dữ khiếu nại đề bài bác tiếp tục cho biết thêm thông số kỹ thuật của độ cao và diện tích S hình tam giác, đòi hỏi học viên tiếp tục tính chừng lâu năm lòng. Nên kể từ công thức tính diện tích S, tớ suy ra sức thức tính chừng lâu năm đáy: a = S x 2 : h

Ví dụ: Cho hình tam giác với diện tích S S vì như thế 4800cm2, độ cao là 80cm. Tính chừng lâu năm cạnh lòng vì như thế bao nhiêu?

Lời giải:

Độ lâu năm cạnh lòng của hình tam giác là:

4800 x 2 : 80 = 120 (cm)

Đáp số: 120cm

Dạng 3: Tính độ cao lúc biết diện tích S tam giác và chừng lâu năm đáy

Cũng kể từ công thức tính diện tích S của hình tam giác, tớ cũng tiếp tục suy ra sức thức tính độ cao của tuồng như sau: h = S x 2 : a

Ví dụ: Cho hình tam giác, biết diện tích S S vì như thế 1125cm2, chừng lâu năm lòng vì như thế 50cm, tính độ cao của hình tam giác cơ.

Lời giải:

Chiều cao của hình tam giác là:

1125 x 2 : 50 = 45 (cm)

Đáp số: 45cm

Bài luyện toán tính diện tích S hình tam giác nhằm bé xíu luyện tập

Dựa nhập những kỹ năng bên trên, bên dưới đấy là tổ hợp một số trong những bài bác thói quen diện tích S của hình vuông vắn nhằm bé xíu hoàn toàn có thể luyện tập:

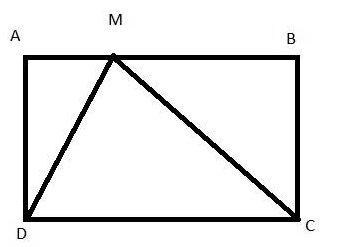
Bài 1: Tính diện tích S tam giác MDC (hình vẽ dưới). lõi hình chữ nhật ABCD sở hữu AB = 20cm, BC = 15cm.

Bài 2: Tính độ cao AH của hình tam giác ABC vuông bên trên A. Biết: AB = 60cm, AC = 80cm, BC = 100cm.

Bài 3: Một hình tam giác sở hữu lòng lâu năm 16cm, độ cao = 3/4 chừng lâu năm lòng. Tính diện tích S hình tam giác cơ.

Bài 4: Một miếng khu đất hình tam giác sở hữu S = 288m2, một cạnh lòng bẳng 32cm. Hỏi nhằm S miếng khu đất gia tăng 72m2 thì nên tăng cạnh lòng đang được cho thêm nữa từng nào mét?

Bài 5: Chiếc khăn choàng hình tam giác sở hữu lòng là 5.6dm và độ cao 20cm. Hãy tính diện tích S cái khăn choàng cơ.

Bài 6: Một quần thể vườn hình tam giác sở hữu S = 384m2, độ cao 24m. Hỏi cạnh lòng là bao nhiêu?

Bài 7: Một loại Sảnh hình tam giác sở hữu cạnh lòng là 36m và cấp 3 lượt độ cao. Tính diện tích S của Sảnh.

Bài 8: Cho hình tam giác vuông ABC (A là góc vuông). lõi chừng lâu năm cạnh AC = 12dm, chừng lâu năm AB = 90cm. Hãy tính diện tích S tam giác ABC?

Bài 9: Cho hình tam giác vuông ABC bên trên A. lõi AC = 2.2dm, AB = 50cm. Hãy tính diện tích S hình tam giác ABC.

Bài 10: Hình tam giác MNP sở hữu độ cao MH = 25cm và sở hữu S = 2dm2. Tính chừng lâu năm lòng NP của hình tam giác cơ.

Bài 11: Một quán ăn kỳ lạ sở hữu hình dạng là một trong tam giác sở hữu tổng cạnh lòng và độ cao là 24dm, cạnh lòng vì như thế 1515 độ cao. Tính diện tích S quán ăn cơ.

Bài 12: Cho tam giác ABC sở hữu lòng BC = 2cm. Hỏi nên kéo dãn BC thêm thắt từng nào và để được tam giac BD sở hữu diện tích S cấp rưỡi diện tích S tam giác ABC.

Bài 13: Một hình tam giác sở hữu cạnh lòng vì như thế 2/3 độ cao. Nếu kéo dãn cạnh lòng thêm thắt 30dm thì diện tích S của hình tam giác gia tăng 27m2. Tính diện tích S hình tam giác cơ.

Bài 14: Một hình tam giác sở hữu cạnh lòng vì như thế 7/4 độ cao. Nếu kéo dãn cạnh lòng thêm thắt 5m thì diện tích S của hình tam giác gia tăng 30m2.  Tính diện tích S hình tam giác cơ.

Bài 15: Cho một tam giác ABC vuông ở A. Nếu kéo dãn AC về phía C một quãng CD lâu năm 8cm thì tam giác ABC phát triển thành tam giác vuông cân nặng ABD và diện tích S gia tăng 144cm2. Tính diện tích S tam giác vuông ABC.

Bí quyết hùn bé xíu ghi lưu giữ công thức tính diện tích S hình tam giác hiệu quả

Đối với kỹ năng tương quan cho tới diện tích S hình tam giác sẽ sở hữu nhiều dạng khác nhau bài bác phức tạp, giống như nhiều nội dung nên học tập. Để hùn con cái lĩnh hội kỹ năng hiệu suất cao, bên dưới đấy là một số trong những tuyệt kỹ nhưng mà cha mẹ hoàn toàn có thể tìm hiểu thêm thêm:

Nắm dĩ nhiên những kỹ năng cơ phiên bản và công thức tính diện tích S tam giác

Bố u hãy thông thường xuyên đánh giá kỹ năng về môn học tập hoặc riêng rẽ lẻ phần diện tích S hình tam giác nhằm hiểu rằng năng lượng học hành của trẻ con cho tới đâu. Cụ thể, test đề ra những câu chất vấn tương quan cho tới công thức tính diện tích S của hình tam giác ngẫu nhiên, coi bài bác vở của con cái,….

Thông qua quýt việc này tiếp tục giúp cho bạn hiểu rằng bé xíu học hành ra sao, phần nào là con cái còn yếu đuối nhằm tổ chức chỉ dẫn và gia tăng lại kịp lúc.

Xây dựng nền tảng toán học tập vững chãi cho tới bé xíu nằm trong Monkey Math

Với toán hình chắc rằng nếu như không tồn tại cách thức dạy dỗ học tập chính, trẻ con tiếp tục cực kỳ nhanh chóng ngán, giống như cảm nhận thấy việc học tập khá khó khăn. Chính nên là, sẽ giúp đỡ con cái sở hữu sự hào hứng rộng lớn nhập lúc học toán thưa công cộng, toán hình thưa riêng rẽ thì cha mẹ hoàn toàn có thể lựa chọn Monkey Math nhằm sát cánh cùng theo với trẻ con.

Monkey Math là ứng dụng học tập toán giờ đồng hồ Anh tiêu xài chuẩn chỉnh Mỹ nhập giảng dạy dỗ Toán học tập so với học viên thiếu nhi, tè học tập và trung học tập (Common Vi xử lý Core State Standards) với những chuyên mục chủ yếu như:

• Đếm và Tập hợp ý số (Count và Cardinality)

• Phép tính và Tư duy Đại số (Operations and Algebraic Thinking)

• Số và Phép tính hệ Thập phân (Number và Operations in Base Ten)

• Đo lường (Measurement)

• Hình học tập (Geometry)

• Thống kê và biểu đồ gia dụng (Data và Graph)

Bên cạnh cơ, nội dung bài học kinh nghiệm đều được xây dựng bám sát lịch trình GDPT mới nhất của Sở GDĐT thể hiện. Tất cả được phân thành nhiều Lever, cá thể hóa theo đòi từng giới hạn tuổi nhằm cha mẹ đơn giản và dễ dàng lựa lựa chọn phù phù hợp với chuyên môn của bé xíu.

Để tạo nên sự hào hứng Khi cho tới bé xíu học tập toán, lực lượng Chuyên Viên của Monkey đang được kiến thiết những bài học kinh nghiệm với trong suốt lộ trình chuyên nghiệp từ coi Clip bài bác giảng minh họa dễ nắm bắt, cho tới học tập và ôn luyện qua quýt những sinh hoạt tương tác và thực hiện bài bác luyện bên trên sách hỗ trợ Monkey Math Workbook (Không bắt buộc).

Với con số bài bác giảng, sinh hoạt khổng lồ lên đến mức 400+ Video bài bác giảng; rộng lớn 10.000 sinh hoạt tương tác; 60 chủ thể không giống nhau dựa vào 7 chuyên mục toán học tập chính. Tất cả đều được minh họa rõ rệt với hình hình họa ngộ nghĩnh, tiếng động chân thật, sinh hoạt thú vị. Chính điều này bé xíu tiếp tục cảm nhận thấy yêu thích rộng lớn lúc học luyện.

Hơn thế, Monkey Math là phần mềm học hành 2 trong một. Khi vừa phải hùn bé xíu cách tân và phát triển suy nghĩ toán học tập hiệu suất cao, vừa phải hùn lựa chọn học tập giờ đồng hồ Anh một cơ hội bất ngờ nhất, Khi lịch trình học tập đều thể hiện tại trọn vẹn vì như thế 100% giờ đồng hồ Anh.

Tải Monkey Math cho tới Smartphone Android

Tải Monkey Math cho tới Smartphone iOS

CLick bên trên trên đây nhằm nhận tư vấn Monkey Math miễn phí

Cùng bé xíu thực hành thực tế thông thường xuyên

Học song song với hành là nhân tố cần thiết không thể không có. Việc thực hành thực tế ở trên đây đó là nằm trong bé xíu thực hiện bài bác luyện nhập SGK, nằm trong con cái mò mẫm hiểu thêm thắt nhiều dạng bài bác luyện không giống nhau về diện tích S tam giác, test mức độ với những đề ganh đua test, tổ chức triển khai những trò đùa học tập toán, tổ chức triển khai những cuộc ganh đua nhỏ nhằm bé xíu nhập cuộc,…

Chính vì như thế được rèn luyện thông thường xuyên, con cái tiếp tục đơn giản và dễ dàng ghi lưu giữ được kỹ năng tôi đã được học tập, biết phương pháp vận dụng nhập thực tiễn và nhất là tạo hình suy nghĩ phát minh nhập quy trình học hành hiệu suất cao rộng lớn.

Ứng dụng của công thức diện tích S hình tam giác nhập thực tiễn

Công thức diện tích S hình tam giác là một trong những trong mỗi công thức hình học tập cơ phiên bản nhất, được dùng trong vô số nhiều nghành không giống nhau của cuộc sống, kể từ toán học tập, vật lý cơ, chuyên môn cho tới phong cách xây dựng, kiến thiết,...

• Trong toán học, công thức diện tích S hình tam giác được dùng nhằm giải những câu hỏi tương quan cho tới hình tam giác.
• Trong vật lý, công thức diện tích S hình tam giác được dùng nhằm đo lường diện tích S của những vật thể sở hữu hình dạng tam giác.
• Trong kỹ thuật, công thức diện tích S hình tam giác được dùng nhằm đo lường diện tích S của những phần tử công cụ, vũ trang sở hữu hình dạng tam giác.
• Trong phong cách xây dựng, xây dựng, công thức diện tích S hình tam giác được dùng nhằm đo lường diện tích S của những dự án công trình phong cách xây dựng sở hữu hình dạng tam giác.

Trên đấy là tổ hợp những trả lời về kỹ năng diện tích hình tam giác. Đây cũng là một trong những dạng toán khá khó khăn và cần thiết nhập quy trình học hành của trẻ con. Vậy nên, cha mẹ hãy nằm trong bé xíu tìm hiểu thêm và tổ chức ôn luyện sẽ giúp đỡ nâng lên hiệu suất cao học hành của con em chất lượng tốt rộng lớn nhé.