1.Một số hệ thức về cạnh và góc trong tam giác vuông
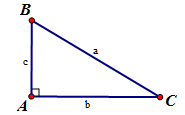
Cho tam giác \(ABC\) vuông bên trên \(A\) đem \(BC = a,AC = b,AB = c.\) Ta có :
\(b = a.\sin B = a.\cos C\); \(c = a.\sin C = a.\cos B;\)
\(b = c.\tan B = c.\cot C\); \(c = b.\tan C = b.\cot B.\)
Trong một tam giác vuông
+) Cạnh góc vuông $=$ (cạnh huyền ) $\times $ (sin góc đối)
$=$ (cạnh huyền ) $\times $ (cosin góc kề)
+) Cạnh góc vuông $=$ (cạnh góc vuông còn sót lại ) $\times $ (tan góc đối)
$=$ (cạnh góc vuông còn sót lại ) $\times $ (cot góc kề).
Chú ý
Trong một tam giác vuông nếu như mang đến trước nhị nhân tố (trong tê liệt đem tối thiểu một nhân tố về cạnh và ko kể góc vuông) thì tao tiếp tục tìm kiếm được những nhân tố còn sót lại.
2. Các dạng toán thông thường gặp
Dạng 1: Giải tam giác vuông
Phương pháp:
+ Giải tam giác là tính phỏng lâu năm những cạnh và số đo những góc phụ thuộc vào dữ khiếu nại mang đến trước của Việc.
+ Trong tam giác vuông, tao sử dụng hệ thức thân thuộc cạnh và những góc của một tam giác vuông nhằm đo lường và tính toán.
+ Các Việc về giải tam giác vuông bao gồm :
Bài toán 1: Giải tam giác vuông lúc biết phỏng lâu năm một cạnh và số đo một góc nhọn.
Bài toán 2: Giải tam giác vuông lúc biết phỏng lâu năm nhị cạnh.
Dạng 2: Tính cạnh và góc của tam giác
Phương pháp:
Bằng cơ hội kẻ thêm thắt đàng cao tao thực hiện xuất hiện tại tam giác vuông nhằm vận dụng những hệ thức thân thuộc cạnh và góc tương thích.